![]() 相似和全等中的动点问题
相似和全等中的动点问题
1.如图,等边三角形![]() 的边长为6,点
的边长为6,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 边上,
边上,![]() ,连结
,连结![]() ,
,![]() 相交于点
相交于点![]() .
.
求证:![]() ,并求
,并求![]() 的度数;
的度数;
若![]() ,求
,求![]() 的值;
的值;
当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,求点
时,求点![]() 经过的路径长.
经过的路径长.
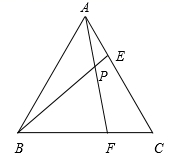
分析:
∵![]() 是等边三角形,∴
是等边三角形,∴![]() ,
,![]()
又![]() ,∴
,∴![]()
∴![]() ,
,![]()
∴![]()
∴![]()
∵![]() ,∴
,∴![]()
又![]() ,∴
,∴![]()
∴![]() ,∴
,∴![]()
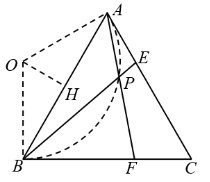
∵![]() ,∴点
,∴点![]() 的运动路径是一段圆弧,该圆弧所对的圆心角为
的运动路径是一段圆弧,该圆弧所对的圆心角为![]()
设圆心为![]() ,连接
,连接![]() 、
、![]() ,作
,作![]() 于
于
则![]() ,
,![]()
∴![]()
∴当点E从点A运动到点C时,点P经过的路径长为: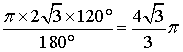
2.已知矩形![]() 的一条边
的一条边![]() ,将矩形
,将矩形![]() 折叠,使顶点
折叠,使顶点![]() 落在
落在![]() 边上的
边上的![]() 点处.
点处.
如图1,已知折痕与边![]() 交于点
交于点![]() ,连结
,连结![]() 、
、![]() 、
、![]() .
.
①求证:![]() ;
;
②若![]() 与
与![]() 的面积比为
的面积比为![]() ,求边
,求边![]() 的长;
的长;
若图1中的点![]() 恰好是
恰好是![]() 边的中点,求
边的中点,求![]() 的度数;
的度数;
如图2,在的条件下,擦去折痕![]() 、线段
、线段![]() ,连结
,连结![]() .动点
.动点![]() 在线段
在线段![]() 上,动点
上,动点![]() 在线段
在线段![]() 的延长线上,且
的延长线上,且![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() .试问当点
.试问当点![]() 、
、![]() 在移动过程中,线段
在移动过程中,线段![]() 的长度是不是发生变化?若变化,说明理由;若不变,求出线段
的长度是不是发生变化?若变化,说明理由;若不变,求出线段![]() 的长度.
的长度.
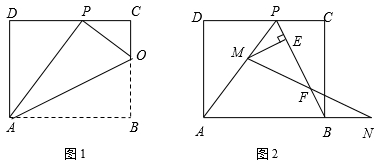
分析:
①∵四边形![]() 是矩形,∴
是矩形,∴![]()
∴![]()
∵![]() 是由
是由![]() 沿
沿![]() 折叠,∴
折叠,∴![]()
∴![]()
∴![]() ,∴
,∴![]()
②∵![]() ,
,![]() 与
与![]()
![]() 的面积比为
的面积比为![]()
∴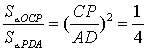 ,∴
,∴![]()
∵![]() ,∴
,∴![]()
设![]() 即
即![]() ,则
,则![]()
在![]() 中,
中,![]()
∴![]() ,∴
,∴![]()
即边![]() 的长为
的长为![]()
∵折叠后![]() 与
与![]() 重合,∴
重合,∴![]() ,
,![]()
∵![]() ,∴
,∴![]()
∵![]() 是
是![]() 的中点,∴
的中点,∴![]()
∵![]() ,∴
,∴![]()
又![]() ,
,![]()
∴![]()
线段![]() 的长度不变
的长度不变

作![]() 交
交![]() 于点
于点![]()
∵![]() ,∴
,∴![]()
∴![]() ,
,![]()
∴![]() ,∴
,∴![]()
![]() ∵
∵![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]()
∴![]()
∵![]() ,∴
,∴![]()
由得:![]()
![]() ,
,![]() ,∴
,∴![]()
∴![]() ,∴
,∴![]() ,∴
,∴![]()







